1955년 여름, 미국인들은 “64,000달러짜리 문제(The $64,000 Question)”라는 새 TV 퀴즈 쇼에 매료되어 있었습니다. 시청률은 무려 85%에 달했습니다. 이 쇼가 얼마나 인기를 끌었냐면, 방영일 저녁 승자를 맞추는데 돈을 거는 도박 시장이 생길 정도였습니다.
이 퀴즈 쇼는 시장의 요구를 충족시키기 위해 동부와 서부 각각의 시간대에 맞춰 따로 방영되었습니다. 얼마 지나지 않아, 일부 도박꾼들은 동부에서 먼저 방영된 쇼의 결과로 서부 사설 도박 업자에게 전화로 미리 배팅해 수익을 올리기도 했습니다.
대부분 그러하듯, 이 쇼도 결국 매력이 떨어졌고, 미국인들은 저녁을 즐길 다른 뭔가를 찾게 되었습니다. 쇼가 종영되자, 사전 배팅으로 빠르고 쉽게 수익을 올리던 도박꾼들의 행운도 끝났습니다.
한편 일반인들에게는 몇 시간 동안의 쇼를 도박꾼들에게는 몇 달러짜리의 도박을 즐기게 해준 이 쇼는 미래의 많은 전설적 투자자들이 사용하게 되는 “도구”를 만들어주게 됩니다.
당시 존 켈리(John Kelly)라는 젊은 과학자는 도박꾼들이 어떤 방식으로 돈을 따는지 알게 되었습니다. 켈리는 스승 클로드 섀넌(Claude Shannon)과 함께 AT&T 벨연구소에서 일하던 젊고 영리한 과학자였습니다. 하지만 켈리는 도박꾼들의 ‘작전’ 방식에 관해서는 별로 관심이 없었습니다. 대신 도박꾼들이 어떻게 베팅 금액을 최적화해 전반적인 수익을 극대화 하는지 알고 싶었습니다.
켈리는 섀넌의 정보 이론의 바탕으로 수학을 이용해 오늘날 “켈리 공식(Kelly Criterion)”이라고 불리는 공식을 만들었습니다. 이 공식의 원리는 도박사가 주어진 확률 대비 자신의 우위를 최적화해 사용하게 되면, 장기적으로 위험은 최소화하는 동시에 기회는 극대화할 수 있다는 것입니다.
즉, “이길 확률을 알고 있다면, 얼마를 걸어야 할까?”라는 질문에 대한 답을 찾은 것입니다.
켈리가 이 공식을 발표하려 하자, AT&T에서는 두 가지 이유로 반대했다고 합니다. 첫째, 켈리가 발표하려 한 논문 제목 “정보 이론과 도박(Information Theory & Gambling)”을 AT&T 경영진이 싫어했다는 것이었고, 둘째, 켈리가 논문에서 언급한 “사설 전화(Private Wire)”라는 용어를 AT&T 고객들이 싫어할지도 모른다는 것이었습니다.
결국 논문은 “정보율에 대한 새로운 해석(A New Interpretation of Information Rate)”이란 제목으로 벨 시스템 테크니컬 저널 1956호에 실렸습니다.
몇몇 전설적인 투자자들이 켈리 공식을 투자에 활용하기 시작했습니다. 특히, 워런 버핏은 일찍 부터 그리고 자주 사용해 왔다고 밝힌 바 있고, 현재도 개인 계좌로 거래할 때 사용하고 있다고 합니다.
모니시 파브라이는 “단도 투자자(Dhando Investor)에서 켈리 공식을 자세히 설명하기도 했습니다. 레그 메이슨에 재직하면서 15년 연속 시장보다 우수한 수익률을 올렸던 빌 밀러 또한 켈리 공식의 오랜 지지자였습니다. 투자 경력 30년 동안 연평균 20%의 수익률을 올렸던 에드 소프 역시 켈리 공식으로 카지노에서 성공을 거둔 후, 월스트리트에서도 적용한 바 있습니다.
간단한 켈리 공식 설명
#
켈리 공식이 완벽한 모델은 아니지만, “성공의 실마리”가 될 수도 있습니다.
켈리 공식을 통해 주어진 승률에 따라 보유 자금 중 어느 정도를 걸어야 하는지 알아보도록 하겠습니다. 켈리 공식을 간단하게 표현하면 다음과 같습니다.

아래 그림처럼 500원짜리 동전을 던져서, 학이 나오면 2천원의 수익, 숫자가 나오면 1천원의 손실입니다. 이 승률에 따라 얼마를 걸어야 가장 알맞은지 알아보기 위한 첫 단계는 아래와 같이 시나리오 만드는 것입니다. 즉, 여기서 시나리오는 학이 나올 경우와 숫자가 나올 경우입니다.
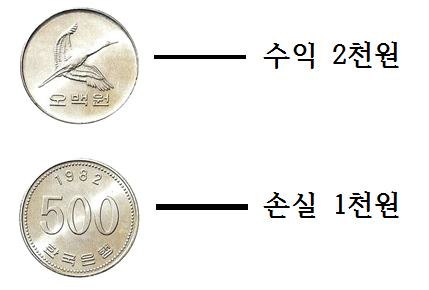
다음 단계는 시나리오에 따른 확률을 확인하는 것입니다. 학과 숫자가 골고루 나오는 동전이라고 할 때, 학/숫자가 나올 확률은 50/50입니다.
위에서 시나리오와 확률을 알았으니, 기대 순이익을 알아낼 수 있습니다. 각 시나리오의 기대 확률(각각 50%)에 수익과 손실(학: 2천원, 숫자: -1천원)을 곱하고, 이 둘을 합하면 기대 순이익을 얻을 수 있습니다. 여기서 기대 순이익은 5백 원입니다.
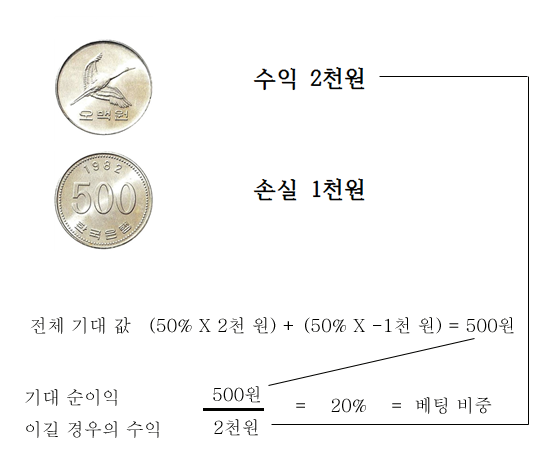
이를 켈리 공식에 적용하면, 가진 자금 중 25%를 걸어야 한다고 나옵니다.
투자에 적용
#
이제 켈리 공식을, 동전 던지기와 달리, 결과를 예상할 수 없는 투자 기회에 적용해 보겠습니다.
삼성전자를 예로 들어 보겠습니다. 현재 삼성전자는 250만원에 거래되고 있습니다. 간단하게 네이버 금융 사이트를 보니, 목표 주가는 약 330만원이고, 52주 최저 주가는 약 200만원 이었습니다. 그리고 양 주가에 도달 확률은 각각 70% 및 30%라고 가정합니다.
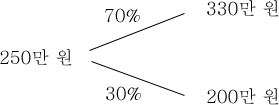
#
다음으로 주가 움직임에 따른 실제 수익과 손실을 파악해 봅시다.

위와 같이 수익과 손실 확률을 얻었습니다. 여기에 동전 던지기의 경우처럼, 시나리오별 확률을 적용합니다.
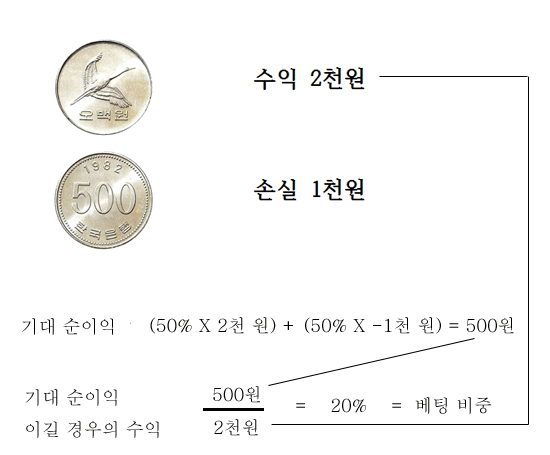
켈리 공식에 따르면, 삼성전자에 보유 자금 중 49.7%를 투자해야 한다고 나옵니다.
하지만, 한 주식에 투자 자금의 49.7%를 투자하기란 쉽지 않은 일입니다. 따라 전체 포트폴리오의 관점으로 접근하는 것이 도움이 됩니다. 이를 위해 전체 투자 자금 중 허용 가능한 최대 손실 규모를 정해 놓아야 합니다. 예를 들어, 투자 자금이 2억 원이고, 이중 15%까지 손실을 감내할 수 있다고 해보죠.
이어서 전체 포트폴리오 규모에 허용 손실률을 곱한 다음, 여기에 켈리 공식으로 얻은 투자 비중을 곱합니다.
계산 결과, 2억 원의 투자 자금 중 삼성전자에 1,775만원을 투자하라고 나옵니다. 전체 포트폴리오 중 약 8.8% 규모입니다. 8.8%도 작은 비중은 아니지만, 켈리 공식에서 나온 58.5% 보다는 합리적인 규모입니다.
켈리 기준의 결함
#
첫째, 아마 가장 큰 결함이라 할 수 있는 점은 “입력하는 수치가 정확해야만 만족할 만한 결과를 얻을 수 있다”는 것입니다. 결과를 얻기 위해 모델에 입력하는 수치가 알 수 없는 미래 사건에 관한 것이기 때문입니다.
위 예에서 삼성전자의 경우처럼, 증권사들이 제시한 목표 주가 330만원이, 그리고 여기에 도달할 확률 70%가 얼마나 정확히 도출해 낸 것이냐에 따라, 이 수치에 도달할 확률이 높아진다는 것입니다.
아이러니한 일입니다. 처음부터 잘 못될 수 있는 두 조건을 깔고 간다고나 할까요.
켈리 공식뿐만 아니라 모든 평가 모델이 안고 있는 결함입니다.
어쩌면 투자의 대가들이 켈리 공식을 통해 수익을 내고 있는 이유는 켈리 공식 덕분이 아니라, 켈리 공식에 대입하는 수치를 비교적 정확히 도출해 낼 수 있기 때문인지도 모릅니다.
둘째, 켈리 공식을 사용하는 당사자의 성격에 따른 편향성입니다. 당사자가 보수적일 수록 결과를 과소평가하고, 낙관적일수록 과대평가하기 마련이기 때문입니다. 어느 쪽이든, 당사자의 편향성이 크면 클수록, 결과는 평균에 회귀하게 됩니다.
셋째, 켈리 공식의 기본 전제가 시작과 끝을 알고 하는 것이라는 점입니다. 존 켈리가 켈리 공식을 고안한 방식은 시작과 끝을 알고 있는 도박에 적용한 것입니다. 여기서 도박사는 도박에서 발생한 수익 또는 손실을 다음번 도박에 포함시킬 수 있습니다.
투자자는 켈리 공식의 결과가 실현되기까지 얼마나 시간이 걸릴지 결코 알 수 없습니다. 즉, 도박에서처럼 투자 자금을 최적화하는데 훨씬 더 어렵다는 뜻입니다.
또 다른 문제는 켈리 공식의 이진적 특성입니다. 돈을 거는 도박과는 달리, 어떤 대상에 투자한 자금을 완전히 날리는 경우는 아주 드뭅니다. 켈리 공식은 미리 양 당간의 결과를 상정하고 시작하지만, 이 상정 자체가 투자에서는 부정확한 가정입니다.
이렇게 전반적으로 켈리 공식은 분명한 결함이 있지만, 유용한 도구인 것도 사실입니다. 유력 투자자들이 사용해 왔고, 앞으로도 계속 사용할 것이라 데는 이유가 있는 것입니다.
This page is synchronized from the post: ‘켈리 공식을 간단히 투자해 적용해 보자’