2003년 11월 25일, 케빈 로렌스(Kevin Lawrence)는 미국 워싱턴 주 역사상 최대 금융 사기 혐의로 20년 형을 선고 받았습니다. 이야기는 이렇습니다.

<케빈 로렌스. 출처: Seattle PI>
케빈 로렌스는 1984년 고등학교를 졸업합니다. 잠시 증권회사에 다니긴 했지만, 곧 관두고 볼링장을 사서 , 최신식 기구와 컴퓨터를 갖추고, 척추 지압사, 마사지사 및 영양사가 있는 피트니스 클럽으로 탈바꿈 시킵니다. 하지만 이것은 사업가로서의 꿈을 이루기 위한 시작에 불과했습니다. 그는 곧 이를 기반으로 최신식 피트니스 클럽 프렌차이즈 사업을 계획합니다. 그리고 투자자들을 모아놓고 이 아이디어를 설명합니다.
로렌스는 이 사업이 피트니스 및 헬스케어를 하나의 비즈니스 모델로 합친 업계의 혁신이 될 것이라고 주장합니다. 즉 클럽 회원들이 같은 곳에서 피트니스 운동도 하고, 건강 관리도 받을 수 있다는 것입니다. 그의 계획에는 피트니스 장비의 디자인, 제조 및 판매도 포함되어 있었습니다. 또한 클럽 회원들의 신체 활동을 분석할 수 있는 소프트웨어도 만들 계획이었습니다.
결국 로렌스는 2천 명이 넘는 투자자를 끌어들여, 1억 달러 가까운 자금을 조달합니다. 훌륭한 이야기꾼 이었음에 틀림 없습니다.
로렌스는 두둑한 투자 자금을 이용해 즈네틱스(Znetix Inc)와 헬스 메인터넌스 센터(Health Maintenance Centre; HMC)를 세웁니다. 이어 운동 선수, 구단 및 이벤트 후원 같은 여러 마케팅 계획으로 즈네틱스를 홍보하기 시작합니다. 즈네틱스는 구단을 인수하고, 호화 파티를 여는 등 돈을 물쓰듯이 씁니다. 이런 행사를 통해 투자자들의 마음속에 즈네틱스가 유명 운동 선수들의 지원을 받고 있으며, 성공 가능한 피트니스 및 건강관리 비즈니스 모델이라는 환상을 심어주는데 성공합니다.
실제로 즈네틱스/HMC가 사업을 통해 수익은 커녕 투자 원금을 회수했다는 증거는 없었습니다. 세금 납부 실적이나 재무 관리 흔적도 없었습니다.
과연 야심찬 젊은이가 잘못된 사업에 망상과 지나친 낙관을 가졌던 것이었을까요? 만일 로렌스가 오로지 사업 홍보에만 돈을 썼다면, 의심을 받지 않았을 것입니다. 하지만, 로렌스와 동료들은 사업보다는 개인적 용도로 돈을 더 많이 썼습니다.
로렌스는 하와이의 집을 포함해 여러 부동산을 구입했습니다. 그는 22대의 개인용 요트(22피트짜리 고속 모터모트 포함), 47대의 명품 자동차(험머 5대, 페라리 4대, 마세라티 2대, 닷지 바이퍼 3대, 캐딜락 에스컬레이드 2대, 람보르기니 디아블로 1대 등), 롤렉스 시계, 여자친구에게 선물한 고가의 다이아몬드 장신구 및 20만 달러짜리 일본도를 가지고 있었습니다.
레오나르드 믈로디노프의 책 “The Drunkard ‘s Walk(번역서: 춤추는 술고래의 수학 이야기)”에서는 로렌스에 대해 이렇게 얘기합니다.

로렌스와 동료들은 투자자들에게 조달한 자금을 여러 은행 계좌와 유령 업체에 복잡하게 분산시켜 마치 사업이 번창하고 있는 듯 속이고 있었다.그들에게는 유감스런 일이지만, 대럴 도렐이란 의심많은 회계사가 7만 건이 넘는 수표 및 전신환을 추적한 다음, 벤포드의 법칙(Benford’s law)을 이용해, 수치의 분포도를 분석 비교했다. 물론 이것은 조사의 시작에 불과했고, 2003년 추수 감사절 마지막날 담청색 죄수복을 입고 변호사를 대동한 케빈 로렌스는 가석방 없는 20년 형을 선고 받았다.
즈네틱스에 대한 조사는 3년 동안 진행됐고, 금융 조사단은 약 12,000시간을 이 조사에 쏟아부었습니다. 조사단은 수천 건의 은행 거래를 추적했습니다. 약 570개의 은행 계좌와 약 60만 건의 수표, 예금 상품 및 전신환을 삿삿이 조사했습니다. 항공기 추락 사고 조사보다 더 지루한 작업처럼 보였습니다. 하지만 12,000시간 중 대부분은 사기가 있었다는 증거를 확인하는 일이었습니다.
진정한 공로는 이례적 현상을 발견했던 대럴 도렐에게 있었습니다. 사실, 로렌스의 비밀을 밝혀낸 것은 도렐이 아니라 “벤포드의 법칙”이었습니다. 그렇다면 벤포드의 법칙은 무엇일까요?
고등학교 1학년 때 수학 선생님은 20문항짜리 4지선다 시험에서 정답을 1번에서 4번까지 각각 5개가 되도록 설계했습니다. 전부 1번만 찍어도 25점은 맞게 되어 있었던 것이죠.
1학기 기말고사 때였습니다. 저희반에서 수학 빵점이 나왔습니다. 수학 선생님을 그 녀석을 교무실로 불렀죠. 그 녀석 왈, 자기 딴엔 더 잘해볼 요량으로 요리조리 찍었다는데, 모조리 정답에서 빗겨나갔던 겁니다. 그리고 한 번호만 찍기에는 자존심이 뭐 어떻다고 했다는…
각설하고 본론으로 다시 돌아와서, 여기서 하고 싶은 말은 인간은 무작위를 직관적으로 이해하지 못한다는 것입니다. 또 인간은 무작위에 쉽게 속습니다. 나심 탈렙은 “행운에 속지마라”에서 우리 세상은 생각보다 더 무작위하다고 밝힌 바도 있습니다.
하지만 벤포드의 법칙에 따르면, 큰 숫자를 모아놓은 데이터의 경우, 우리가 생각하는 것보다 무작위성이 덜하다고 합니다.
즉, 우리 주변에 널린 다양한 수치 자료에서 첫 자리에 가장 빈번하게 나타나는 수는 무엇일까. 얼핏 생각해보면 수치 자료에는 1부터 9가 11.1%씩 동등하게 분포하므로 첫 자리 수도 1부터 9가 같은 비율로 나타날 것 같아 보입니다. 하지만 예상과 달리 1이 가장 빈번하게 나타나고, 2에서 9로 갈수록 그 빈도는 현저히 낮아집니다.

[출처: 네이버 지식백과, 수학산책]
미국의 천문학자 사이먼 뉴컴(1835~1909)은 1881년에 로그표가 담긴 책을 보면서 앞쪽 페이지가 뒤쪽 페이지보다 더 닳아 있다는 것을 발견했습니다. 이는 사람들이 로그표에서 1로 시작하는 값들을 더 자주 찾아봤음을 의미한 것입니다. 물리학자 프랭크 벤포드(1883~1948)는 뉴컴의 이런 발견을 1938년에 공식화했습니다. 벤포드는 강 335개의 넓이, 물리학 상수 104가지, 분자 중량 1800가지 등 20개 분야 자료들의 첫 자리 수 분포를 분석해 ‘벤포드의 법칙’을 내놓게 됩니다.
그렇다면 실생활의 데이터에서는 어떤 의미가 있을까요?
한 마을 또는 한 나라 모든 이들의 연령 데이터를 수집해 본다면, 연령 분포도 벤포드의 법칙을 따를까요?
그렇지 않습니다. 데이터의 범위가 0 내지 122세(세계 최장 수명 기록이 122세이므로)로 아주 작기 때문입니다.
벤포드의 법칙은 큰 숫자가 균일하게 분포된 데이터에서 더 정확하게 적용되는 경향이 있습니다. 일반적으로 자릿수가 큰 수치로된 데이터일수록, 벤포드의 법칙이 더 정확하게 적용된다는 밀입니다.
그렇다면 벤포드의 법칙은 왜 성립하는 것일까요? 네이버 지식백과의 수학 산책에서는 이렇게 설명합니다.
우리 주변의 자료 중에는 일정한 배율로 증가하는 것이 많다. 예를 들어, 일정한 배율로 자라는 나무의 현재 높이를 1이라고 해보자. 높이가 2로 2배가 될 때까지 걸리는 시간을 A라고 한다면, 높이가 2에서 3으로 1.5배가 될 때까지 걸리는 시간은 A보다 짧다. 마찬가지로 3에서 4로 1.33배 늘어나는 데 걸리는 시간은 더 짧다. 결과적으로 나무의 높이는 1에서 머무르는 시간이 길고, 2에서 9로 갈수록 머무는 시간이 짧아진다. 이를 표현한 것이 바로 벤포드의 법칙에 나타나는 상용로그 식이다.
벤포드의 법칙은 회계 부정을 적발하기 위해 1972년부터 사용되기 시작했습니다. 미국의 수학자 마크 니그리니(Mark Nigrini)는 벤포드의 법칙을 이용해 에너지 기업 엔론의 회계 부정을 밝혀낸 것으로 유명합니다.
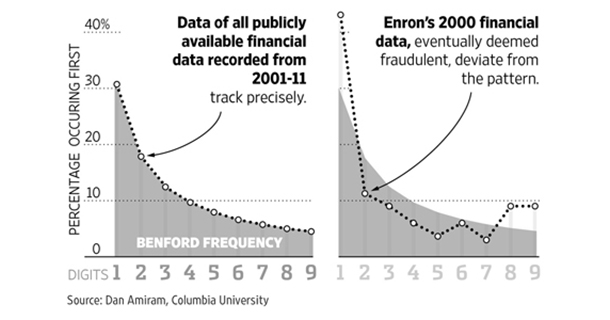
<출처: mhpmag.com>
벤포드의 법칙은 이렇게 기업의 회계 부정이나 가격 담합 등을 적발하는 데도 많이 이용되고 있습니다. 만약 어떤 기업이 부정한 방식으로 수치를 조작하게 되면, 1부터 9까지의 수를 무작위로 균등하게 분포시킬 가능성이 높습니다. 그렇게 되면 첫 자리 수의 빈도가 1에서 9로 갈수록 낮아지는 벤포드의 법칙에 위배되게 됩니다. 이를 이용해 국세청이나 금융감독 기관은 기업의 회계 조작 단서를 잡곤 합니다.
그 밖에 벤포드의 법칙이 사용된 몇 가지 흥미로운 사례가 있습니다.
- 벤포드의 법칙은 2009년 이란 선거에서 부정 선거의 증거로 사용되었습니다.
- 그리스 정부가 유로존에 가입하기 위해 EU에 보고한 거시경제 데이터가 벤포드의 법칙을 통해 조작된 것으로 나타났습니다.
- 한 연구원은 빌 클린턴의 13년치 납세 신고서에 이 법칙을 적용하기도 했습니다.
읽어주셔서 감사합니다!!
This page is synchronized from the post: ‘회계 조작을 찾아내는 벤포드의 법칙’