오늘 스팀잇 재단에서 나온 글입니다.
Improving the Economics of Steem: A Community Proposal
한글 번역본은 @ayogom님께서 이미 작성해 주셨습니다: 스팀의 경제 개선 : 커뮤니티의 제안
이 포스팅에서는 3가지 제안 중 첫번째인, 선형 보상에서 수렴 선형 보상으로의 이동 부분만을 다루겠습니다.
자세한 식이나 수치를 다루기에 앞서서, 일단 이 보상 공식을 바꾸려는 이유부터 알아봅시다.
재단측의 주장은 다음과 같습니다:
스팀파워의 수익 극대화에만 관심이 있는 사용자는 신중한 큐레이션을 통해 플랫폼에 이익을 주는 대신 셀프 보팅이나 보팅봇에 임대를 주곤 합니다. 수렴 선형 보상으로 변경할 경우,
- 더 적은 수의 포스팅에 보팅이 집중되게 인센티브가 주어질 것이고, 그러면 이렇게 비생산적인 (counterproductive) 한 행위가 더 잘 보일 것이다.
- 다수의 계정으로 스팀파워를 나눠서 대응할 수 있으나, 이럴 경우 수익률이 악화될 것이다.
이런 이익 추구 행위를 막을 수는 없으나, 수익률을 낮출 수는 있다.
이게 왜 현실성이 떨어지는지, 그리고 오히려 해가 될 수 있는지 이제 분석해 보겠습니다.
이렇게 이름도 어려운 수렴 선형 보상에 관한 제안은 이 글에 별도로 설명되어 있습니다: 링크
이게 무슨 소리인지 이해하려면 일단 “수렴 선형 보상” 부터 알고 가야 합니다. 그러면 그 전에, 선형 보상과 초선형 보상에 대해서 먼저 알아야 합니다.
“선형 보상” 은 f(x) = x 로 이해하면 됩니다.
내가 받은 보팅들의 “스팀파워” (엄밀히 말하면 rshares 수치이지만, 스팀파워라고 이해해도 큰 문제 없을 것이기에 이 글에서는 rshares와 스팀파워, 스파를 같은 의미로 사용하겠습니다) 에 비례해서 보상이 책정됩니다. rshares가 2인 글은 1인 글보다 2배 더 보상을 받는거죠. 지금의 스팀잇 보상 체계가 이렇습니다.
“초선형 보상” (superlinear) 은 f(x) = x^2으로 이해하면 됩니다.
rshare가 2인 글이 1인 글보다 2배 넘는 보상을 받는 겁니다. 대표적으로 스팀잇 초기의 제곱보상이 있죠. 제곱보상의 경우 rshares가 3인 글은 1인 글의 보상의 3^2 = 9배를 받게 됩니다.
대부분의 경우, 선택안들은 장단점을 가지고 있습니다. 그러면 선형 보상과 초선형 보상의 장단점 이라고 주장되는 것들은 무엇일까요? 간단히 요약하면 다음과 같습니다.
선형 보상의 장점: 이해하기 쉽다. 보상이 정비례하므로 “공평” 하다.
선형 보상의 단점: 다계정으로 스파를 나누어서 셀봇을 많이 하거나 보팅봇을 쓰기 쉽다.
초선형 보상의 장점: 한 계정으로 스파를 모으게 유도하므로, 그 계정의 행동만 “감독” 하면 된다.
초선형 보상의 단점: 스파가 적은 계정들의 보팅들이 의미가 많이 줄어든다.
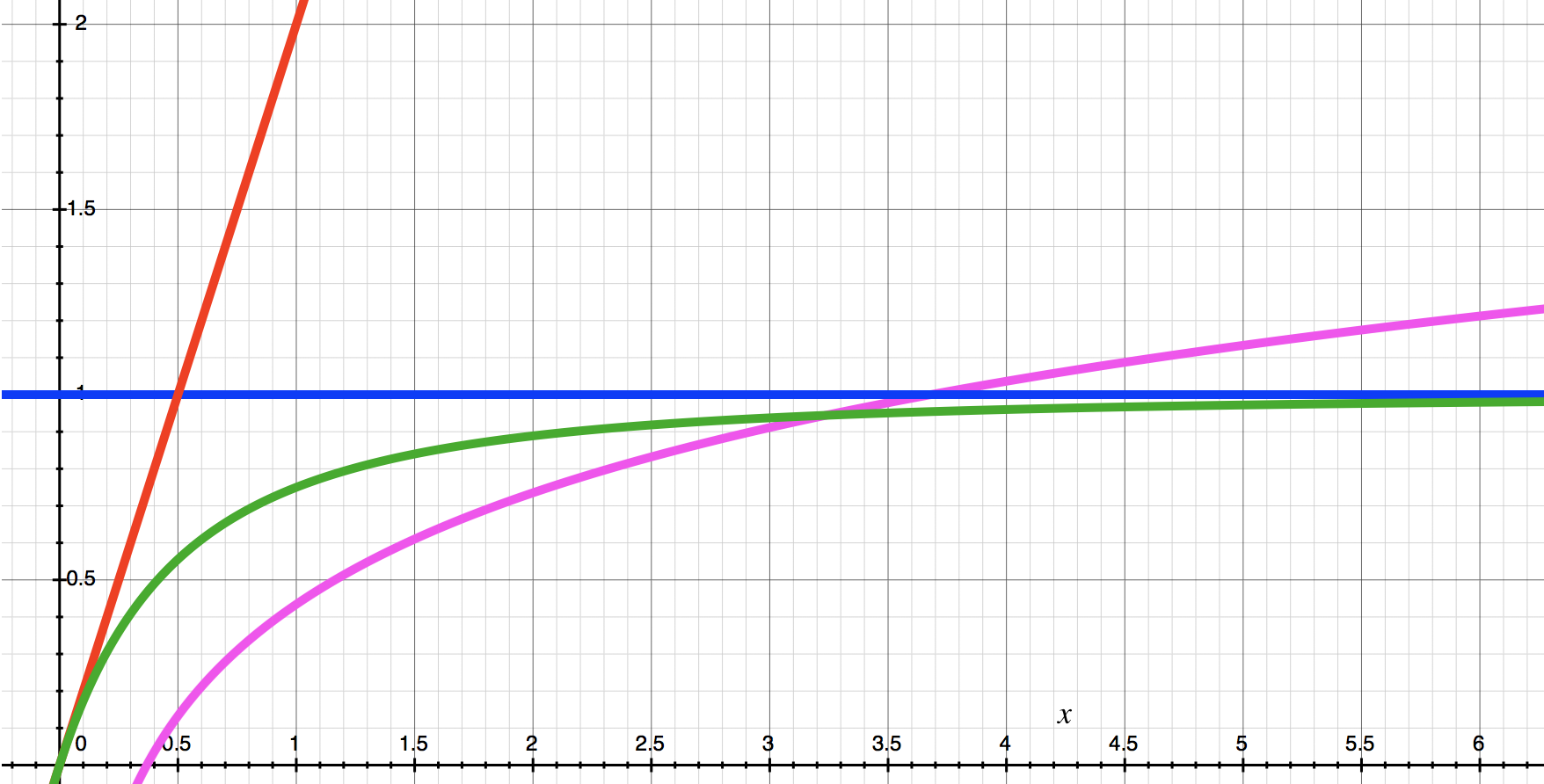
그래서 두 보상 형태의 장점을 합한 것이 “수렴 선형 보상” 이라고 주장하고 있으며, 글쓴이가 예로 든 것은 f(x) = x^2 / (x+1) 형태입니다. 이 형태는, 초기에는 초선형 보상과 비슷하다가 x가 커질수록 선형 보상에 근접하게 됩니다. 그래프로는 이렇지요 (@ayogom님 글에서 가져옵니다):
Source : https://steemit.com/steem/@vandeberg/reward-curve-deep-dive
빨간색 : n^2
파란색 : n
녹색 : n^2 / (n + 1)
분홍색 : n log( n )
빨간 선과 같은 초선형보상은 스파가 커질수록 스파당 보상이 기하급수적으로 커지며,
파란 선과 같은 선형보상은 스파의 크기에 무관하게 스파당 보상이 일정하며,
초록이나 분홍 선과 같은 수렴 선형 보상은 스파가 작을 때는 초선형 보상과 비슷하고, 스파가 커지면 선형 보상 형태에 수렴합니다.
자, 그럼 이게 왜 현실성이 떨어지거나 오히려 해가 될 수 있을까요?
1. 스파가 낮은 유저들의 보상을 더욱 줄인다:
수렴 선형 보상은 초기에는 초선형 보상과 거의 같습니다. 달리 말해서 스파가 낮은 범위에서는 보상이 더 줄어듭니다. 스파 1과 10이 예전에는 보상이 1:10이었다면 이제는 1:100이 되는거죠. 구체적인 변수 값들에 따라 조금씩 달라지겠지만, 기본적으로 이 형태가 되면 스팀잇 초기 진입 뉴비들이나 스파업 안한 분들은 보상이 정말 0에 수렴할겁니다. 실제로 제곱보상일때 스팀잇을 겪으셨던 분들은 아마 잘 아실듯.
2. 한 계정으로 스파가 모여서 그 계정의 행위만 감시하면 되면, 그 계정의 행위를 제제할 수 있는가?
특정 계정의 행동을 제제하는 것이 옳고 그른지는 둘째치고, 제제를 하는게 옳다고 하더라도, 지금 보팅봇이나 고래 계정(버니라던가…) 들의 행위를 몰라서 못 막고 있나요? 이건 눈가리고 아웅입니다. 상당수의 증인들마저 보팅봇 사업을 하거나 셀봇 또는 부계정들을 이용한 사실상의 셀봇을 하고 있는 판에 말이죠.
3. 보팅봇이나 보팅풀 형태를 오히려 장려합니다.
내가 1만 스파를 가지고 있고, 나는 수익 극대화에 관심이 있다고 합니다. 이럴 경우 보팅풀에 합류하는것이 (보팅봇도 일종의 보팅풀이므로 보팅풀에 대해서만 논하겠습니다) 지금보다도 더 이익입니다. 간단한 예로 1만 스파를 가진 사람 10명이 모여서 스파임대로 10만 스파 계정을 하나 만들고 그 스파 계정에게 하루에 한번 10만 스파짜리 풀봇을 받는 것이, 각자 1만짜리 스파로 셀봇 10번 하는것보다 수익률이 더 좋으니까요. 지금 선형 보상 형태인데도 각종 형태의 보팅풀이 넘쳐나고 성업중인데 (참고로 저는 이게 맞고 틀리다는 이야기를 할 생각은 전혀 없으며, 저도 참여하고 있는 스팀엔진 각종 토큰들은 지금으로는 보팅풀과 크게 차이가 없다고 생각합니다) 이렇게 되면 더더욱 보팅풀이 늘어날 것이고, 그러면 스파가 적거나 신규 유저의 경우 더욱 받을 보상이 줄어들게 될 겁니다.
보상의 불공평함, 아니 보상이 최적화되지 않은 방식으로 (“최적화” 의 개념도 애매한데, 스팀 가격의 상승 또는 지지, 아니면 유저 수의 증가를 의미한다고 하겠습니다) 분배되고 있기에 이를 고치려는 시도는 좋은데, 문제는 적어도 이 “수렴 선형 보상”은 현실성이 없고 오히려 다른 문제를 생기게 하거나 기존 문제를 악화시킬 것으로 보입니다.
게다가 이해하기도 힘들죠. 룰이 뭔지를 알아야 논의를 할텐데, 룰 자체도 이해하기 힘들면 이건 그냥 아웃입니다.
한 걸음 더 나아가 봅시다. 사실 선형 보상이 아니면, 대부분의 경우 “어뷰징” 이 존재합니다. f(x)=x^2 같은 초선형 보상의 경우 보팅풀을 장려한다고 위에 썼었지요? 초선형 보상의 반대인 f(x) = sqrt(x) 같은 형태는, 계정 쪼개기로 어뷰징이 가능합니다 - 1만 스파 대신에 100스파짜리 계정 100개로 서로 돌려가며 보팅하면 됩니다. 이건 어쩌면 “활성 유저” 를 늘리기엔 좋을 수도 있겠군요.
이 중간에 있는 이런저런 형태도, 변수에 따라서 최적값이 달라질 수는 있으나 결국 특정 스파를 보유하는게 가장 이익이 되는 구간이나 지점이 존재하고 (예를 들어서 1000스파), 그러면 딱 그만큼의 스파를 보유하게 부계정들로 쪼개거나 아니면 여러 계정들을 합해서 그만큼의 스파를 보유하는 보팅풀을 만드는 “어뷰징” 이 가능하죠.
“공평” 하게 보상을 나누는 것은 기본적으로 존재하기 힘든 것이지만, “신규 유저 영입” 이란 목적조차도 달성하기 어렵게 하거나 고래들에게 가는 보상이 더 커지는 형태로 바꾸려는 이유는 사실 잘 모르겠습니다.

This page is synchronized from the post: ‘“수렴 선형 보상” 은 현재 문제 해결에 도움이 안된다.’